The Detailed propagation course

HTML Propagation Fundamentals - Fixed Link Propagation - Mobile Propagation

PDF Fixed Links Propagation - Mobile propagation

Short and simple (the old tutorial)

Propagation in Free Space - Absorption by Atmospheric Gases - Diffraction over Terrain - Refraction and Ducting - Reflections - Troposcatter - Rainscatter - Sporadic E

First, what do we mean by propagation in free space?

Free space is a region where these is nothing - the vacuum of outer space is a fair approximation for most purposes. There are no obstacles to get in the way, no gases to absorb energy, nothing to scatter the radio waves. Unless you are into space communications, free space is not something you are likely to encounter, but it is important to understand what happens to a radio wave when there is nothing to disturb it.

In free space, a radio wave launched from a point in any given direction will propagate outwards from that point at the speed of light. The energy, carried by photons, will travel in a straight line, as there is nothing to prevent them doing so. For all practical purposes, a radio wave when launched carries on in a straight line forever traveling at the speed of light.

As the energy in a radio wave goes on propagating forever without loss, why do people talk about "free space loss" ?

Free space loss is not really a loss at all. It relates to the intensity of the wave at a distance from the source measured by some standard collector, like an antenna or a telescope. As the wave spreads out, the intensity becomes lower.

Consider a radiowave source that radiates in all directions with equal intensity from a single point (like a light bulb). How much energy can be collected by an antenna at some distance away from the source?

All the points at a given radius r from a single point form the surface of a sphere and the total energy is uniformally spread out over the area of this sphere (remember our source is radiating equally in all directions). So the amount of energy that can be collected over the section of the total area represented by our collector is proportional to the ratio of the "capture area" of our collector to the total area.

The area of this sphere is proportional to the radius:

The power per unit area is simply the total power divided by the total area. If the power is measured in watts this is:

This power is usually referred to as the power flux density:

For example, at a radius of 8.9m, the total area of the sphere is 1000 square m. Over a collecting area of 1 square m, only 1/1000th of the total energy is to be found. This represents "loss" of 1000, equivalent to 30 dB.

All the above is fairly obvious first year secondary school maths, but it is a bit more complicated owing to convention. It is rather awkward thinking about collecting areas when what you actually know is the loss relative to some standard - usually something mythical like an isotropic radiator. This is an antenna that radiates equally in all directions which is naturally, impossible to build.

Generally, what we really want to know is how much energy gets from one antenna to another. The amount of power collected by an ideal antenna is simply the power flux density multiplied by the effective capture area of the antenna Ae.

Which we can write as:

The effective capture area of an antenna is related to the gain of the antenna. If the Gain of the receiving antenna is Grx the following holds:

So:

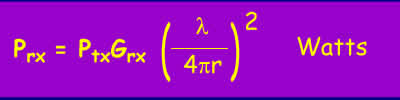
Normalising this to a receiver antenna of unity gain so Grx =1, the ratio of the received power to the transmitted power which is the proportion we "lose" on the path is called the free space loss represented by:

This is a dimensionless figure and is usually expressed in dB.

Here are Some useful equations:

Free Space Loss = 32.5 + 20log(d) + 20log(f) dB, Where D is the distance in km and f is the frequency in MHz

Free Space Loss = 92.5 + 20log(d) + 20log(f) dB, Where D is the distance in km and f is the frequency in GHz

and for the Americans:

Free Space Loss = 36.6 + 20log(d) + 20log(f) dB, where D is the distance in miles and f is the frequency in MHz

© Mike Willis December 26th, 2006