Free space in this context means space with nothing at all in it, it does not exist in the known universe but interstellar space is a good approximation. We start at this level as there is nothing there to make the maths even more complicated than it already is.

 

The important features of free space: Uniform everywhere Contains no electrical charge Carries no current Infinite extent in all dimensions

OK - so now we have to deal with Maxwell's equations, or at least just mention them. You can skip this bit if you are one of those people with a pathological fear of algebra, you will miss out a little, but that is just the way it is.

Maxwell's equations

Radio waves are predicted to propagate in free space by electromagnetic theory, they are a solution to Maxwell's Equations.

 

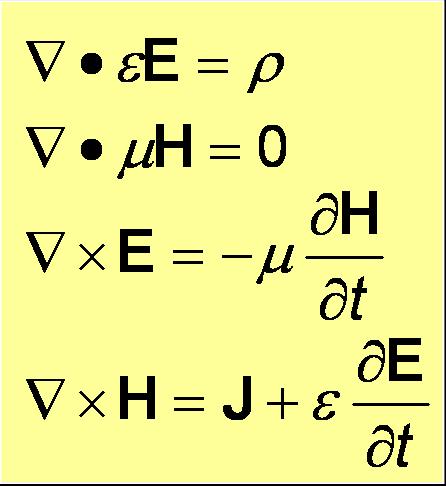
James Clerke Maxwell (1831-1879) was an interesting character. His first paper to the Edinburgh Royal Society “On the Description of Oval Curves, and those having a plurality of Foci” was written when he was only 14 and  had to be read out for him because he was too young. It was based on work he had done using twine, pins and a pencil. Besides his famous work on Electromagnetic theory, he was a leading contributor to the kinetic theory in gases and to the theory of colour vision. He correctly discovered how we perceive colour and took the first colour photograph, an image of of a Tartan Ribbon in 1861 using 3 coloured filters, red, green and blue to capture and later project 3 copies of the image.

E = Electric vector field
H = Magnetic vector field
ρ = charge enclosed = 0 in free space
J = current density = 0 in free space

These are really not that bad, firstly, E and H Fields:

Also Note

 

The Divergence operator          Ñ×E       Ñ×H

 

 

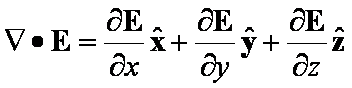
In physical terms, the divergence of a three dimensional vector field is the extent to which the vector field flow behaves like a source or a sink at a given point.

tells us lines of Electric flux, are proportional to the electric field and "diverge" away from a region containing electrical charge. Electric field lines which do not form closed loops begin and end on charge

tells us lines of Magnetic field never diverge from anything, and so must form closed loops. (because there is no “magnetic charge”)

 

Now for the Curl operator         ÑxE      ÑxH

 

 

 

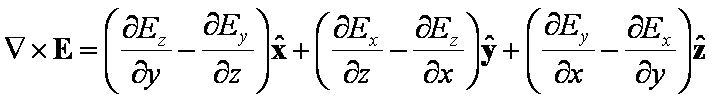
This is the tendency of the vector field to loop or rotate in space. The curl shows a vector field's rate of rotation: the direction of the axis of rotation and the magnitude of the rotation.

tells us electric field lines which form closed loops, encircle (curl) a changing magnetic field.

tells us magnetic field lines H form loops which encircle both conduction current density J, and also "displacement current density" (dE/dt) which is generated by time-varying electric fields. The current density J flowing out of a region ("diverging") must result in a decrease of charge within the region. In free space there is no charge and so J = 0.

Maxwell’s equations show that looping E field with give rise to a change in the H field and a looping H field will give rise to a changing E field. This is very important, an electromagnetic wave is a solution to Maxwell's equations. Fortunately, we can get a long way without solving Maxwell’s equations ourselves..

Next