Free Space Loss

We all now know that:

So how can we talk about a loss ?

Actually, this last“forever” statement is not quite true, the energy is carried by photons that do eventually decay but as the half life of a photon is of the order of 6.5 Billion years, we don't need to worry about it.

We can’t really talk about free space loss, but we do anyway…

What is means is the ratio of the received power to the transmitted power,

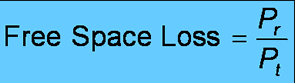
this not really a loss at all, energy is conserved, it is just that usually not all of it is captured at the receiver.

We can easily predict the free space loss from the well known equation:

- it is important to understand where this comes from. Imagine a light bulb in free space, light spreads out more or less equally in all directions

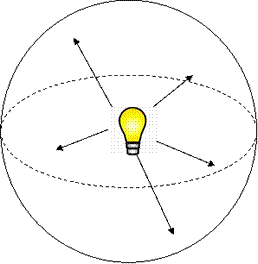
The wavefront expands as a sphere and the energy flux radiates outwards at the speed of light.

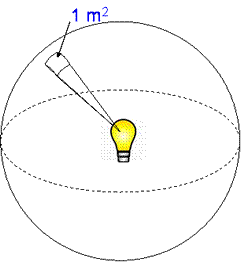
The Power Flux Density (PFD) is the power per unit area is the power from the bulb divided by the area of this sphere. The area of a Sphere = 4πr², So:

Which demonstrates that in free space, field strength is inversely proportional to range and hence power which is proportional to the square of the field strength is inversely proportional to the square of the range. (This is a simplistic explanation and possibly stating the obvious, however it has been included just in case the inverse square law is not obvious it everyone.)

An Example

Voyager 1 is a space probe which is now 15 billion km from Earth (USA billions). How strong are its transmissions at the Earth?

The transmitter power is about 13 watts at 8415MHz. The 3.7m antenna has a gain of 48 dB which makes this an effective power in our direction of 800kW.

This is covered soon, but the effect of a large dish is to focus the energy to only fill a small segment of the sphere around the object. This forms a cone, the area of the face of a cone still expands with the square of the distance.

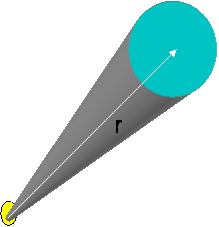
The power density at Earth is from the previous equations:

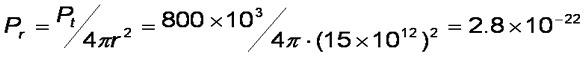watts per square metre

Voyager is received by the large 70m dish at Goldstone. A 70m dish has an area of 3800m, so the total power it receives over that area is ~ 1 x 10^-18 W – about an attowatt. One attowatt is not very much (-180 dBW). We will come back to this later when we cover link budgets

Voyager 1 is nearly 30 years old, it was launched on 5^th September 1977 from Cape Canaveral from a Titan-Centaur rocket. While the rocket used a lot of fuel, the overall consumption is now up to about 30 000 mpg and getting higher. It is now the most distant man made object at 100Au distance from the sun and heading away at 3.6Au per year. 1Au is the radius of the Earth Orbit. It is so far away that light takes nearly 14 hours to make the trip.

The influence of the sun at this range is 10000 times smaller –  so there is no hope at all for solar power. Instead, the spacecraft gets its power from a radioactive source, which decays producing heat which is in turn converted into electricity.  This source now produces 290W compared to 470W at launch. There are also liquid propellants for station keeping, the spacecraft has 28kg left which should last at least to around 2020. It will reach the Heliopause in 2015, effectively leaving the solar system.

Goldstone Observatory is located in the Mojave Desert, California, USA. It was set up in the late 1950s to communicate with the Pioneer space missions.

The observatory is part of NASA's Deep Space Network. There is a 26 metre antenna which was built to support the Apollo missions in the 1960s. There are five 34m dishes, four of which are high efficiency using beam waveguides and one very large 70m dish which is used to communicate with distant missions like Voyager. It has a communications range of about 16 billion km. For Voyager, the normal data rate for telemetry is 160bits/second with a maximum data rate of 1.4kb/s.

Deriving the FSL equation

This is sometimes referred to as the Friis formula. We start with the equation for received power flux density,

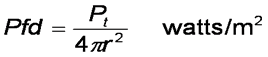
To find the power received, we multiply by the effective area of the antenna

The effective area A_e of an antenna is related to its gain

Substituting:

rearranging:

Remembering:

In useful units of MHz, dB and km

Which after putting in the constants and correcting for units of MHz and km leads us to the standard result:

Next