

The Fundementals
Introduction Maxwell's equations Plane waves Free space loss Gas Loss Refraction Diffraction Reflections Troposcatter Rain effects Vegetation Statistics Link budgets Noise Multipath Measurements Models
Tropospheric Scattering
Air is not uniform, there are eddies, thermals, turbulence etc. where the air has slightly different pressure and hence a different refractive index. The eddies have outer scales ~100m and inner scales of ~ 1mm. Energy that is fed into a turbulent system goes primarily into the larger eddies and from these, smaller eddies are shed. This process continues until the scale of the turbulence is small enough for viscous action to become important and dissipation as heat to occur.
The variations have a spectrum, the Kolmogorov spectrum
with a slope proportional to K-11/16.
The effect of these irregularities on the wavefront is for the waves to be scattered and defocused.
It is a very slight effect and Energy is scattered by very small angles, but over long paths this leads to Troposcatter propagation. Signals may be scattered to receiver beyond the horizon. This mechanism is the dominant mode for long range VHF/UHF propagation.
The Common volume formed by the intersection of the antenna patterns is important. The common volume needs to be in the troposphere, so there is a limit to the propagation range.
A typical value for the loss by this mode, for a 250km 150MHz path with 20 dBi antennas is ~140dB (see later) - THIS INCLUDES ANTENNA GAIN. The line of sight loss would be ~80dB, including antenna gain, Troposcatter is 65 dB below line of sight in this case, but very few terrestrial paths this long are line of sight.
The median loss is given by:
L = M + 30log(f) + 10log(d) + 30log(θ) + LN+ LC - Gt - Gr
This is an empirical model, with M is typically 19-40 dB depending on climate.
θ is the scatter angle (milliradians) - Note how the loss increases dramatically with θ, LN accounts for the height of the common volume, LC is the aperture-medium coupling loss and Gt , Gr are the gains of the antennas.
q = q e + q t + q r
Where q t and q r are the transmitter and receiver horizon angles and
q e = 1000 d/ReRe = effective earth radius ~ 4/3 x 6370km.
The value of M varies between 19dB and 40 dB depending on the climate In the UK the usual values are M=33 dB for overland paths and M=26 dB for paths over the sea.
LN accounts for the transmission loss variation with the height of the common volume (there is less air higher up).
LN = 20log(5 +gH) + 4.34gh
Where H = 10-3 qd/4 and h = 10-6 q2 Re/8 and g is a climatological parameter ~0.27 km-1 in the UK.
LC is the aperture to medium coupling loss taking account of the common volume variation with antenna gain:
LC = 0.07 e0.055(Gt + Gr)
It is possible to calculate Troposcatter loss for other percentage of time values using a correction factor:
L(p) = L(50 - Y(p)Where Y(p) = C(p)Y(90)
p |
50 |
90 |
99 |
99.9 |
99.99 |
C(p) |
0 |
1 |
1.82 |
2.41 |
2.9 |
Y(90) again depends on climate and location
Y(90) = - 2.2 - (8.81 - 2.3x 10-4 f)e-0.137h over land
Y(90) = - 9.5 -3e-0.137h over sea
Going the other way, to lower time percentages down to around 20%, the distribution is symmetrical so:
L(p) = L(50) - {L(100-p) - L(50)} when 20 < p <50
Examples
Frequency 144 MHz, Antenna Gains 16 dBi path length 250km. Horizon angle in both cases = 0 milliradians - i.e. looking horizontally.
q = qe = 1000 x 500 / (1.333 x 6370) = 29.4 milliradians
M = 32, H = 1.84, h = 0.92, LN = 15.9, LC = 0.41
so L(50) = 149 dB
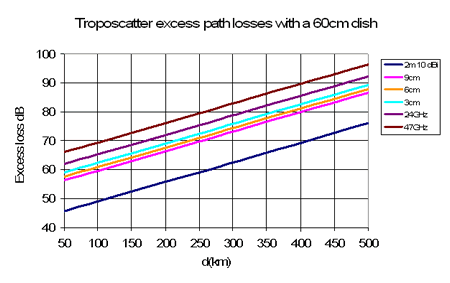
Another example predicting troposcatter path loss for systems operating in the WiMAX bands from 2.4 to 42GHz is shown below. This is based on the ITU-R P452 model, which should strictly only be used for interference assessment. Excess loss here is the extra loss compared to a line of sight path.
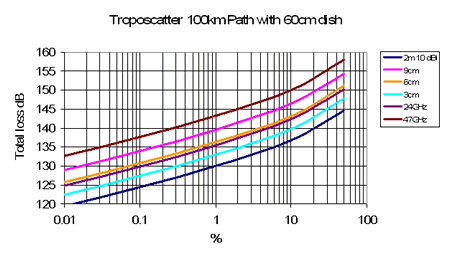
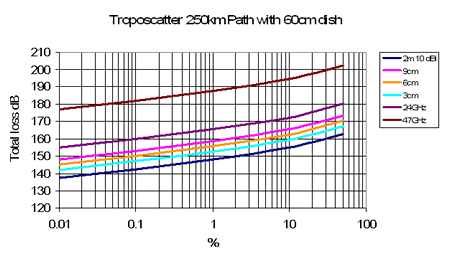
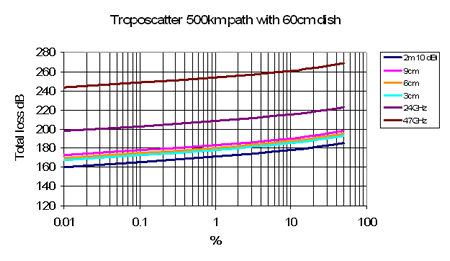
Another example, total loss for a 100km troposcatter path, here 145MHz 10 dBi antennas, otherwise 60cm dish, 70% efficient.
Scintillation
Scintillation is a rapid variation in the signal amplitude. One of the causes is tropospheric irregularities and the amount of scintillation depends on the wavelength compared to the eddy size. This effect is present all the time, (twinkle twinkle little star) and although tropospheric scintillation is generally not significant for terrestrial systems below 40GHz it is important for low elevation satellite links where there is a handy formula for predicting it:
Where G(r) is an aperture averaging factor that depends on the radius of the antenna and the wavelength, ε is the elevation angle and f = frequency in GHz. G(r) can be calculated from:
Where:
D = antenna diameter
η = antenna efficiency
h = height of turbulence, 1000m
Re = effective earth radius 8500km
Molecular scattering
Molecular scattering is an important mechanism too and becomes more so at higher frequencies from 1000GHz up. Remember that the energy in a radiowave is quantified into discrete packets of energy called photons - wave/partial duality etc. The energy of the photon is related to the frequency of oscillation e = hf, where h is Plank's constant. When considering the scattering of high frequency radiowaves, it is often more convenient to think in terms of photons.
Rayleigh Scattering: When photons are of wavelengths comparable to the the size of gas molecules, scattering occurs. The most common mode of scattering is elastic scattering where energy is not transferred from the photon to the molecule. This type of scattering is called Rayleigh scattering. This scattering increases with the fourth power of the frequency, which incidentally is why the sky is blue.
Raman scattering: It is also possible for photons to interact with gas molecules in an inelastic manner so that energy is transferred between the photon and the molecule. This is called Raman scattering and this is of particular importance to optical communications systems.
At higher photon energies incident photons can excite vibrational modes polarised molecules. This is an energy transfer process with the resultant emission of a scattered photon of lower energy (i.e. lower frequency/higher wavelength) and leaving the molecule in a higher energy vibrational mode. Only certain vibrational mode energies are allowed and by inference, only discrete frequency/wavelength differences can occur. The spectra of the resultant scattered photons forms a set of spectral lines at discrete offsets from the original frequency/wavelength called "Stokes lines". It is also possible for a molecule to give up some of its energy to an incident photon and thereby increase the photon energy. Again, this forms a discrete set of lines, the "anti-Stokes lines".
© Mike Willis May 5th, 2007