The plane wave equation:

An diagram of a plain wave is shown below:

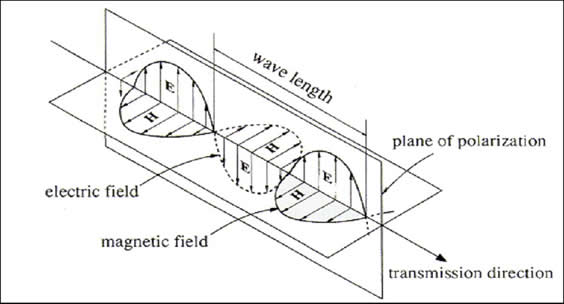
The solution to Maxwell's equations for a plane wave are:

We are not going to do the maths for this in any detail but if we substitute the above functions of E and H into Maxwell's equations we can show that they work. E and H are orthogonal, as shown by the unit directional vectors, and also have a sinusoidal variation in amplitude. By convention the polarisation is defined by the direction of the E field. The wavelength is the distance traveled in one cycle of E and H. The existence of plane waves was predicted by John Henry Poynting in 1884. To put it exceptionally crudely, a looping Electric field causes a looping magnetic field which causes a looping Electric field etc. and effectively the Electromagnetic wave propagates like a perpetual game of leapfrog.

John Henry Poynting (1852–1914) pictured below, was a physicist and a professor of physics at Mason Science College which is now part of the University of Birmingham.

We can derive some relationships from the plane wave solution that will be useful later. The field strength can be expressed as:

Where ω = 2πf (the angular frequency)

k = the wave number, the rate of change of phase with distance:

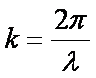
The wave number k is frequently found in EM theory, it describes the variation with distance along the propagation axis whereas ωt is the variation with time. The ratio of E to H is the impedance of free space (by Ohms law):

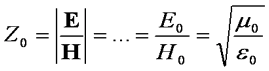
The impedance of free space, which is equal to 377 Ohms. is an important figure as it tells us the relationship between the E and H field strengths.

The Poynting vector

The Poynting vector usually written as S is the direction in which energy travels in an EM wave, we will not go into the vector calculus, but it is given by taking the cross product of the vector field of E and the complex conjugate of the vector field H.

This represents a power flow along the z axis. The average in watts per square metre is given by:

The phase velocity is the rate along the z axis that a point of constant phase moves,

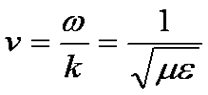which is the speed of light and is approximately 3x10⁸ m/s in free space

and the wavelength is the velocity divided by the frequency:

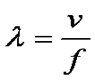
The Exponential Notation

It is also possible for us to express E and H in exponential notation:

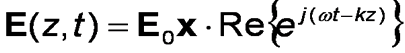
Where Re{} means take the real part. This comes from the equivalence e^jx  =  cos(x)  +  j sin(x)

All this is very useful as by using this notation differentiation in easy because the differential of e^jx  =  -je^jx. It basically makes the maths of the plane wave equation easier because of the relative ease of taking the differential. From the point of view in question, i.e. Maxwell's equations we get:

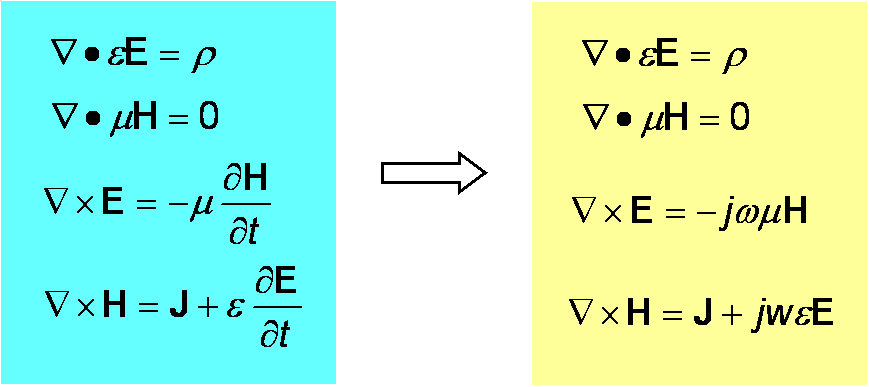
We have effectively got rid of the tedium of finding the differentials which makes a big difference.

Losses in materials

All materials that are not free space are lossy to some extent or another. The amplitudes of the E and H fields decay exponentially with distance along the direction of propagation:

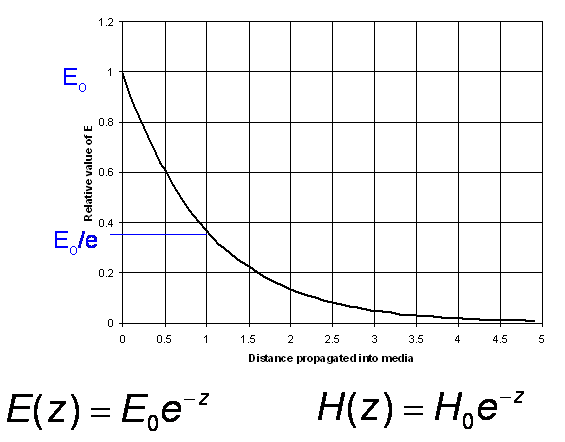
We can write this mathematically as:

where Lz represents the loss with distance. The rate of decay here is important – it is exponential, so a wave propagating through a Lossy medium can be described as having a specific attenuation in terms of decibels per metre.

E.g. a length of coaxial cable or waveguide will have a loss specified in dB per metre. A one metre length might be specified to lose 1 dB. This is a 25% loss. A 2 metre length will not lose 50%, it will lose 2 dB which is 40%. Obvious, but important.

Refractive Index

We are used to learning about refractive index in optics. Remember the wave number

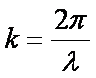
We can see this depends on the material because the wavelength λ depends on the speed of light in the material. We could actually write

k = nk_o   where n is the refractive index and k_o is the value of k in free space. The refractive index is the ratio of the speed of light in free space to the speed of light in the medium, i.e. n = c/v.

Using the exponential notation:

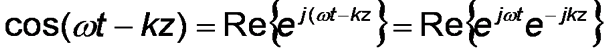
So...

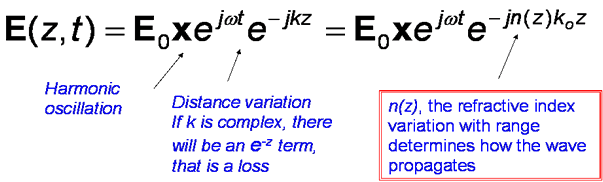
This notation is useful as we can often forget about the harmonic oscillations, assume they carry on minding their own business confident that they will still be there when we need them, while concentrating our algebraic skills on what happens with distance.

Now on to some applications.

Next