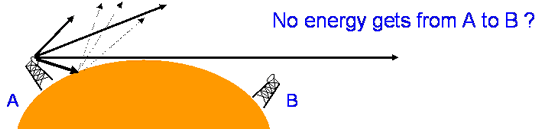
You might imagine waves travel along straight lines for ever, or until they hit something. For a transmitter on the ground power radiated above the horizon will go into space, Horizontally beamed signals will travel to the horizon and then be absorbed, signals below horizontal will be absorbed or scatter into space.

Rule of thumb – distance to radio horizon (km) versus transmitter height (m) d = 4.12√h

We know signals do propagate beyond the horizon and the major mechanisms are:

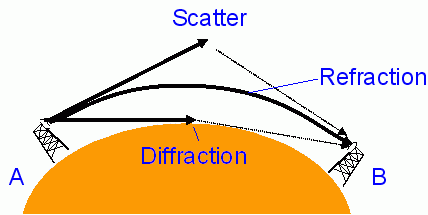
Atmospheric Refraction

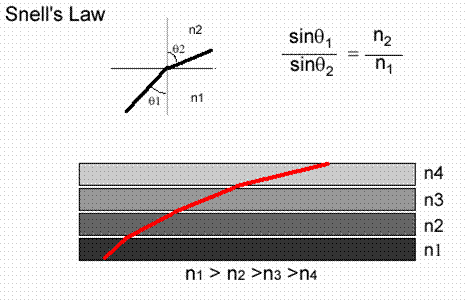
To understand refraction, which is the atmospheric bending of the radio path away from a straight line, we need to remember Snell's law.

 

 

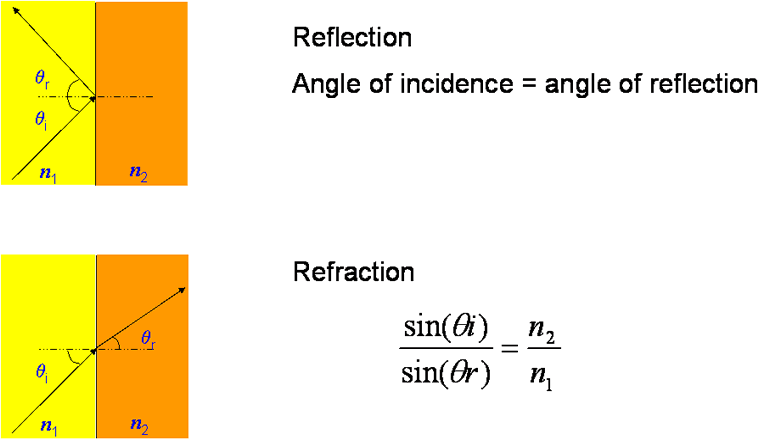
Willebrord Snel van Royen (1580–1626) was a Dutch astronomer and mathematician and is most famous for his law of refraction now known as Snell's law. In 1617 he reported on an experiment to measure the distance between Alkmaar and Bergen op Zoom which are separated by one degree with the aim of determining the radius of the Earth. He measured one degree to be equal to 107.4 km. which was only 3km out. He also developed new method for calculating π. He discovered his law of refraction in 1621.

Refractive index vs Height

As we move to higher altitudes we have lower pressures and lower temperatures. As a result the refractive index falls with height.
Radio waves get “bent” downwards and are able to propagate beyond the geometric horizon, which extends range.

   

To find out how much we need to know how the refractive index of air varies with height. This requires the introduction of a new unit, for reasons that become obvious.

N - Units

The refractive index of air is very close to 1. Typically n = 1.0003 at sea level and this is most tedious - there are lots of decimals that must be used because the detail is important, so we define a new unit, the N unit

N is typically 310 at sea level in the UK. The value of N can be calculated from:

Where:

The dry term depends only on pressure and temperature, the wet term also depends on the water vapour concentration. The temperature, pressure and water vapour pressure vary with time and space.

Pressure falls exponentially with height, the scale height, where it drops to 1/e of the sea level value is around 8km. This value of e is not the water vapour pressure, it is the constant e from natural logs and has the value 2.718. Scale heights are used frequently in describing functions that decrease exponentially.

Temperature falls by 1^oC/100m in the first few km above sea level.

Water partial pressure is much more complex, it is strongly governed by the weather and is limited to the saturated vapour pressure. Because the water vapour pressure is governed by the amount of moisture the air can hold, once the temperature drops below 0C the water vapour condenses out as clouds. The saturated water vapour pressure is around 40 mbar at 300K (a warm day) and 6mbar at 273K (freezing). The zero degree isotherm is typically at a few km in altitude, near the cloud base. Practically, we can say the amount of water vapour above 2-3km is negligible.

The result is that the refractive index falls exponentially with height in a “standard” atmosphere. The scale height is ~7.4km and in the first 1000m we can approximate this as a straight line with a slope ~ -40 N/km.

 

 

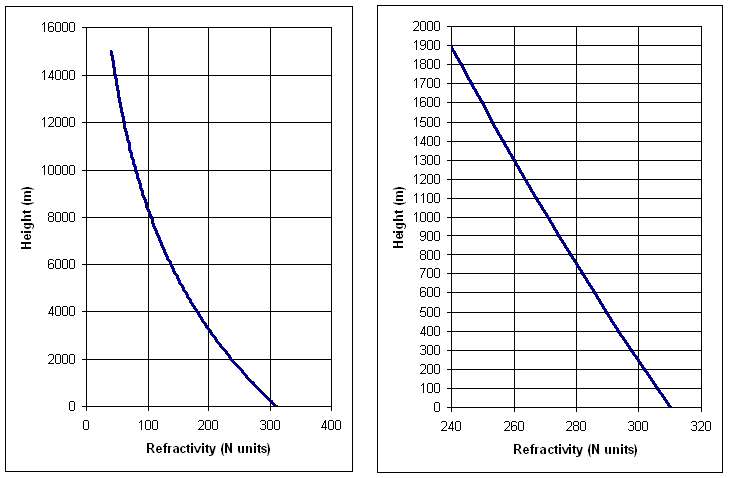
Representing an exponential function as a straight line is cheating, but it is a good enough approximation up to 1000m or so. Beware of this when planning systems on top of mountains.

 

Super-refraction

If dN/dh exceeds -157 N units, signals will be refracted by more than the curvature of the Earth and be trapped. We call this super-refraction.

N typically falls by 40 units per km of height which we call the lapse rate of N.

The rate of change of angle dθ/dh ~ dn/dh ~ dN/dh x10⁶ which we find from Snell’s law and applying the small angle approximation sin(θ)~tan(θ)~(θ) and

The radius of the Earth is ~ 6371 km. To follow Earth curvature, dθ/dh needs to exceed the rate of change of curvature of the earth, which is found to be -1.57x10-4 radians/km if you do the maths. Remember N units are a million x ( refractive index - 1). So dN/dh = -157 N units/km is required for a radio wave to just follow Earth.

The equivalent Earth radius

Many models are simpler if we can treat radio waves as if they were traveling along straight lines in a standard atmosphere (dN/dh = -40)
We can achieve this by pretending the Earth has a larger radius which we call the equivalent Earth radius R_e.

Typically R_e = 4/3 R in the UK and we define the “k factor” k such that R_e = k R.

Having done this we can then look at paths by drawing straight lines rather than curves across a terrain profile. The ability to draw straight lines is practically, very important. It simplifies propagation prediction software used in link planning. Nobody does it by hand any more. The image shows a path profile where line of sight is blocked. The red ovals show the Fresnel ellipsoids, in this case the first. These will be covered when we come on to study diffraction, but the practical point is that for a link to be line of sight, no-terrain should enter into the Fresnel ellipsoid.

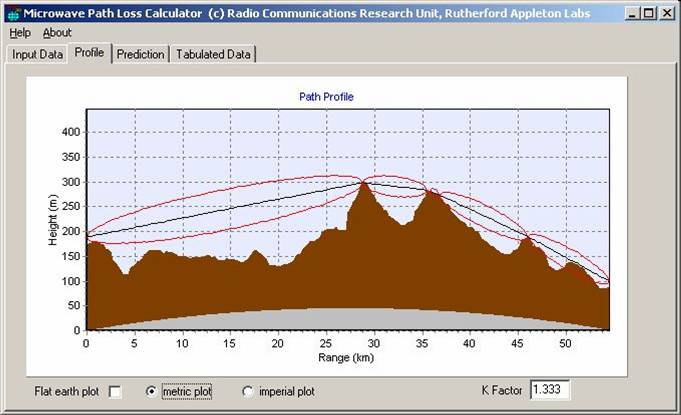
Example of a path profile
(note the red curves represent Fresnel zones, to be covered later)

 

Ducting and Inversions

 

Non-standard atmospheres can lead to anomalous propagation. Pressure tends to be quickly restored to equilibrium and most important are variations in the water vapour concentration and temperature. Ducts tend to form when either Temperature is increasing or water vapour concentration is decreasing unusually rapidly with height. For example:

 

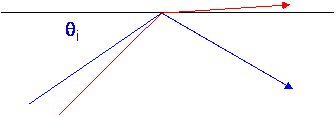
Ducts can occur either at ground level or elevated and depending on the terminal height the signal may or may not couple into the duct. To couple into and remain in a duct the angle of incidence must be small, typically less than 1^o.

  

 

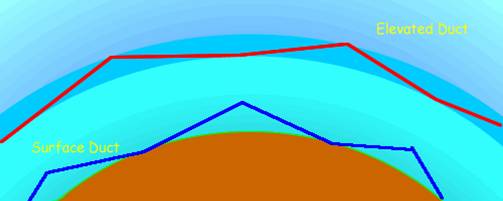
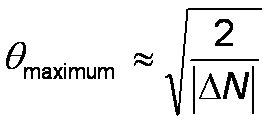
Duct depth and “Roughness” are also important. If the duct depth is small compared to the wavelength, energy will not be trapped. If the roughness is large compared to the wavelength, energy will be scattered out of the duct. Surface ducts have the ground as a boundary and energy will be lost to the terrain, vegetation etc.

 

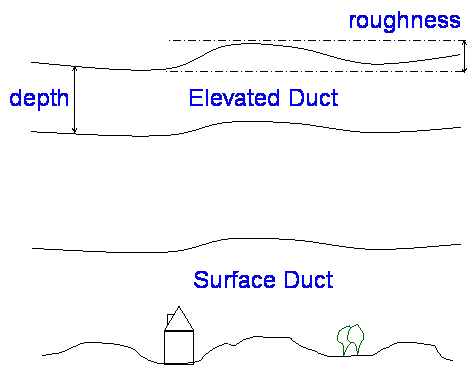
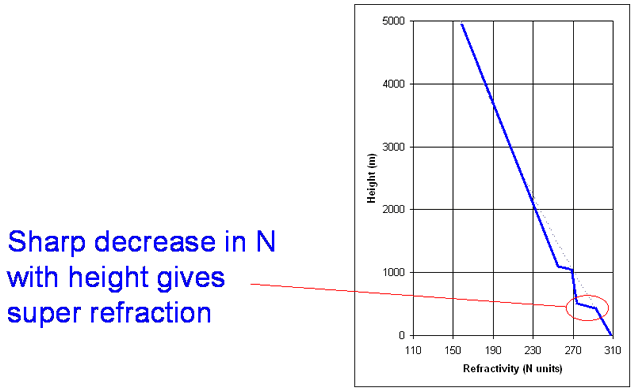
The significance of elevated ducts is that they can allow signals to propagate for very long distances over the horizon. It is possible for intermediate terminals to be below the elevated duct and not able to couple into it – resulting in non-monotonic path loss with range.

A good example of the temperature inversion occurred on 7th November 2006. Strong inversions like this are unusual in the UK.

  

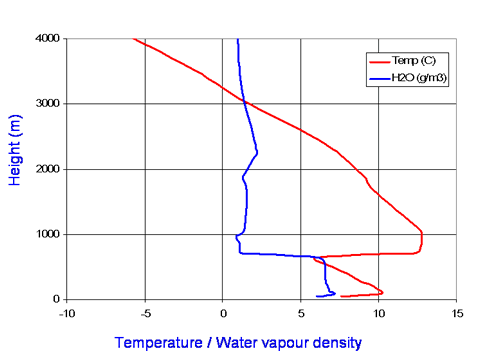
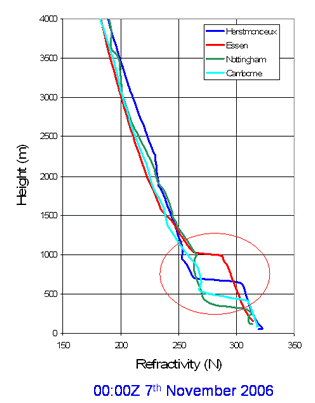
The refractivity profiles (http://weather.uwyo.edu/upperair/sounding.html) show a widespread sharp decrease in N with height gave rise to strong super-refraction. This caused some interesting anomalous propagation effects and long range interference to services.

What causes conditions like this?

Causes of Ducting

Briefly the weather alters temperature pressure and humidity regions of air are moved about, mixed up, elevated and depressed by cyclones and anti-cyclones, heated by the sun and cooled by radiation at night.

Evaporation Ducts

There is usually a region for a few metres above the surface of the sea where the water vapour pressure is high due to evaporation. This also occurs over large bodies of water, for example the great lakes. The thickness of the duct varies with temperature of the location, typically 5m in the North sea, 10-15m in the Mediterranean and often much more over warm seas as in the Caribbean and Gulf. Naturally, these ducts have a significant effect on Shipping and have been extensively researched. It is the reason that VHF/UHF propagation over sea can extend to great distances causing all sorts of international frequency co-ordination problems.

Temperature Inversions

Usually, temperature falls with height by about 1K per 100m. On clear nights the ground cools quickly and this can result in a temperature inversion, where the air temperature rises with height.

Solar radiation heats up the ground and Radiation from the land raises the air temperature near ground, this warm air rises. On clear nights the ground cools very quickly, also cooling the air close to it, this results in cool air close to the ground with warm air above it soon after sunset this is a temperature inversion.

If it is dry, the temperature term is dominant and super refraction and ducting can occur. This is particularly common in desert regions.

If there is significant water vapour the relative humidity can quickly rise to 100% and vapour condenses out as fog. This condensation reduces the water vapour density near the ground leading to cold dry air near the ground, warmer moister air above and results in sub-refraction. This can lead to multipath on otherwise apparently perfectly good line of sight links.

Subsidence

This is a mechanism that can lead to elevated ducts and is associated with high pressure weather systems - anticyclones. Descending cold air forced downwards by the anticyclone heats up as it is compressed and becomes warmer than the air nearer the ground leading to an elevated temperature inversion. (Atmospheric pressure always increases closer to the ground unless someone has let of a bomb above you). This all happens around 1-2km above the ground far too high to cause ducting except for very highly elevated stations as the coupling angle into the duct is too great for a ground based station. As the anticyclone evolves the air at the edges subsides and this brings the inversion layer closer to the ground. A similar descending effect happens at night. In general, the inversion layer is lowest close to the edge of the anticyclone and highest in the middle. Anticyclones and subsequent inversions often exist over large continents for long periods.

Advection

This is the movement of air masses, typically occurring in Early evenings in the summer with air from a warm land surface advecting over the cooler sea. This warm air mixes with the cooler air which is relatively moist through being close to the surface of the sea. This leads extending the height of the evaporation duct and to high humidity gradients and a temperature inversion forming a surface duct within the first few 100m above the sea. These ducts do not persist over land and are a coastal effect. Typically in the UK they are associated with warm anticyclonic weather over the continent of Europe and advection out over the north sea. They tend to be weaker than subsidence ducts but do occur relatively often over the North Sea and can persist for many days. For example, it is relatively common for UHF signals to propagate well beyond line of sight from the East coast of England across the North Sea to the low countries.

The picture below shows what the ITU-R consider to be the global incidence of ducting. It replaces an earlier model that only used Latitude.This really does still need to be tested some more as it may be more of a reflection of Matlab plotting routines for sparse data than actual reality. Use with care.

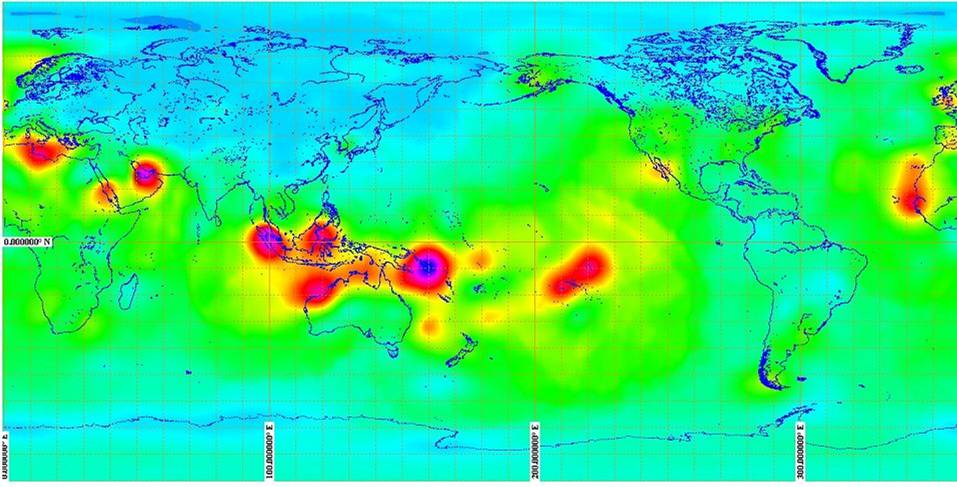
The original model was very crude:

 

As good UK citizens we are most concerned with the UK probability of ducting. Evaporation ducts - happen all the time and a widespread duct frequently forms over the sea, e.g. North Sea - UK - Low countries. Surface ducts occur for around 6% of time, they tend to be up to 300m in height and cover ~100km. This is a fairly low incidence as surface ducts occur for around 50% of the time in the Gulf, they are not really anomalous there.

Elevated ducts exist for around 7% of time, they occur up to 3km in altitude, and cover ~100km. Again this is low incidence as elevated ducts happen for 40% of the time in Gulf.

Next